Important calculations using subnets

Suppose your Windows computer is set up as follows:

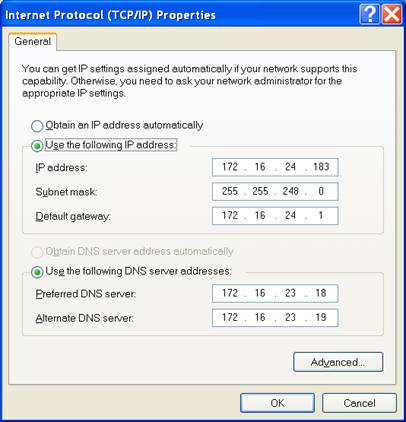
Question 1. Describe this computer's subnet using CIDR (i.e. with a forward slash) notation.

Solution:

First we write out the IP address and subnet mask in hexadecimal and binary notation:

	Decimal	Hexadecimal	Binary
computer’s IP address	172.16.24.183	AC.10.18.B7	1010 1100 . 0001 0000 . 0001 1000 . 1011 0111
Subnet mask	255.255.248.0	FF.FF.F8.00	1111 1111 . 1111 1111 . 1111 1000 . 0000 0000

We see there are 21 ones in the subnet mask, so the subnet description will end with “/21”. But we still need to work out the address of the subnet. To do this, apply the subnet mask to the computer's IP address, using a bitwise AND operation. This gives:

	Decimal	Hexadecimal	Binary
Subnet address	172.16.24.0	AC.10.18.00	1010 1100 . 0001 0000 . 0001 1000 . 0000 0000

So final answer is 172.16.24.0/21.

Question 2. What is the maximum number of interfaces that can be accommodated on this subnet?

Solution:

IP address is 32 bits, but in this case 21 of them are dictated by the subnet address. That leaves 11 bits for assigning addresses to interfaces, so the maximum number of interfaces is 2^11 = 2048.

Question 3. What is the largest IP address that can be accommodated on this subnet?

The first 21 bits must be the same as the subnet address, i.e. 1010 1100 0001 0000 0001 1xxx xxxx xxxx. To make the rest of the address as large as possible, we fill in the rest of the bits with ones. Then convert to hexadecimal and decimal:

	Decimal	Hexadecimal	Binary
Largest IP address	172.16.31.255	AC.10.1F.FF	1010 1100 . 0001 0000 . 0001 1111 . 1111 1111

Final answer: 172.16.31.255